Definition Of Delta Derivatives

Delta can be used for a number of purposes including gauging risk exposure and hedging. If D is a distribution we want to define another distribution D its distributional derivative.

This Is A Definition From A Kindle Dictionary Dictionary Definitions Full Definition

This done by declaring D by D f D f.

Definition of delta derivatives. This technical definition leads to an approximation for the behavior of a portfolio. Video created by Ruinan Liu and Vipul Naik. Then the function f x is said to be differentiable at x0 and the derivative of f x at x0 is given by f x0 lim Δx0 Δy Δx lim Δx0 f x0 Δx f x0 Δx.

We will also look at the first part of the Fundamental Theorem of Calculus which shows the very close relationship between derivatives. We do this by taking the limit as Delta-x approaches zero. Delta is a risk sensitivity measure used in assessing derivatives.

The derivative of f x f x with respect to x is the function f x f x and is defined as f x lim h0 f x hf x h 2 2 f x lim h 0. Delta is no longer just an arbitrary range around x. Delta expresses the amount of price change a derivative will see based on the price of the underlying security eg stock.

What we want to do is decrease the size of Delta-x as much as possible. Δ p deltaΔ s. Δx is a variable.

Delta Δ represents the rate of change between the options price and a 1 change in the underlying assets price. In my opinion the easiest way to understand it is that theyre dual vectors of a function space. In the limit assuming the limit exists we will find the exact slope of the tangent line to the curve at the given point.

Its an arbitrary range around xh. Using the same notation the delta distribution is defined as deltaf f0. Now we can define distributional derivatives.

And ε is of course the range of f xs around the limit point L but in this case the output f x is going to be the slope over the interval xh. The figures on the left derive from 7and show δ representations of ascending derivatives of. In other words the price sensitivity of the option is relative to the underlying.

The sensitivity measure is equal to the change in the derivative value as a ratio of the change in the underlying assets price. Formal Definition of the Derivative Let f x be a function whose domain contains an open interval about some point x0. Am I supposed to be graphing h as a function of 2xh.

In this section we will formally define the definite integral give many of its properties and discuss a couple of interpretations of the definite integral. This value is the derivative. Simplified derivation of delta function identities 7 x y x Figure 2.

Note that unlike the usual jargon no integral appears in the definition. If youre trying to use lHôpitals rule you need to differentiate with respect to Δx and the derivative of a variable with respect to itself is 1. The reason that in physics you can get away with pretending it is zero is that delta and its derivative delta arent actually functions with a converging Fourier expansion in the first place but as they are often called distributions.

Since we want this to be a distribution and again without reference to an integral we find given our partial-integration rule that deltaf -deltaf equiv -f0 which is the definition of the derivative of the delta distribution. Delta is the first partial derivative of a portfolios value with respect to the value of the underlier. Delta can be positive or negative being between 0 and 1 for a call.

The Dirac delta functionδx is often described by considering a function that has a narrow peak atx 0 with unit total area under the peakIn the limit as the peak becomes infinitely narrow keeping fixed the area under the peak the function. Note that we replaced all the a s in 1 1 with x s to acknowledge the fact that the derivative is really a function as well. But using lHôpitals rule doesnt help here anyway because that requires knowing the derivative of sine.

More generally the n -th distributional derivative D n of D is defined by D n f 1 n D f n. F x h f x h.

Epsilon Delta Definition Of A Limit Fully Explained

Epsilon Delta Limit Definition 2 Limits Differential Calculus Khan Differential Calculus Calculus Math

An Extensive Explanation About The Epsilon Delta Definition Of Limits Calculus Studying Math Definitions

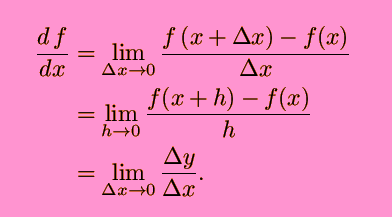
World Web Math Definition Of Differentiation

Limits L Hopital S Rule And Epsilon Delta Definitions Essence Of Calculus Chapter 7 Youtube Calculus Mathematics Essence

Pin By Chris Mizell On Calculus I Definitions Precalculus Calculus

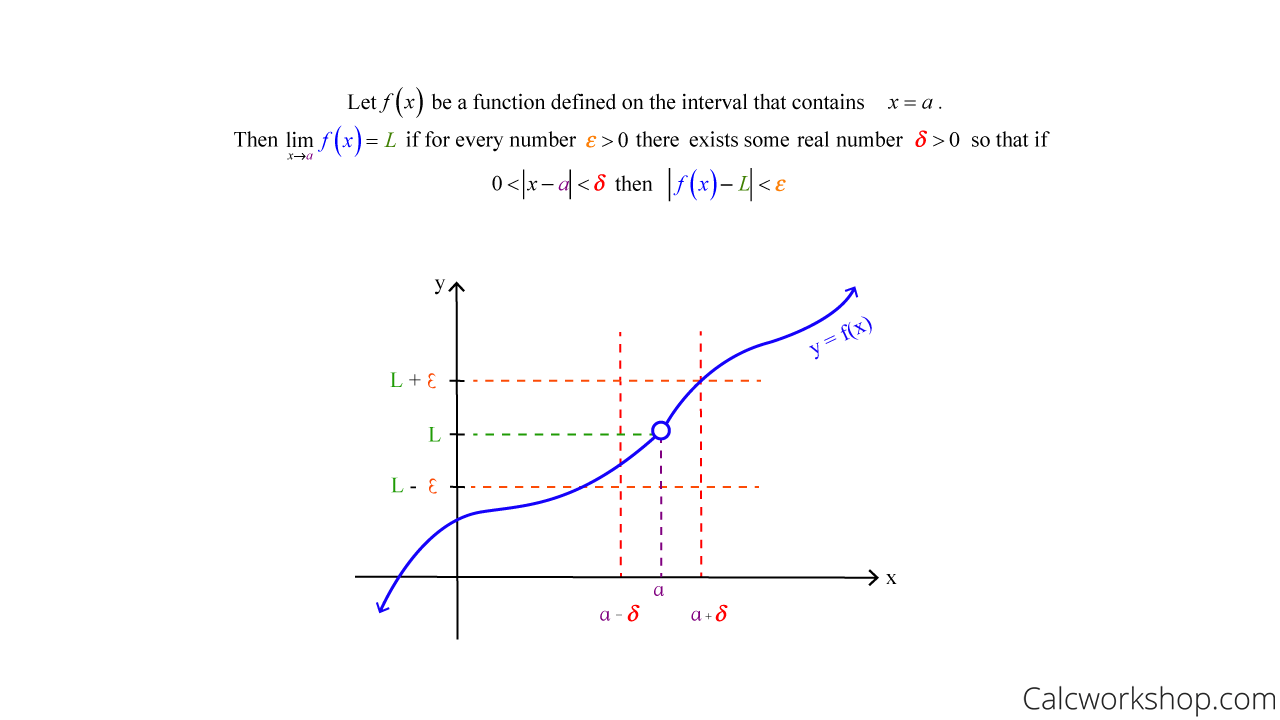
Epsilon Delta Definition Of A Limit Fully Explained

What S So Special About Euler S Number E Essence Of Calculus Chapter 5 Youtube Calculus Studying Math Logic Math

Limit Definition Of A Derivative

Limit Definition Of A Derivative

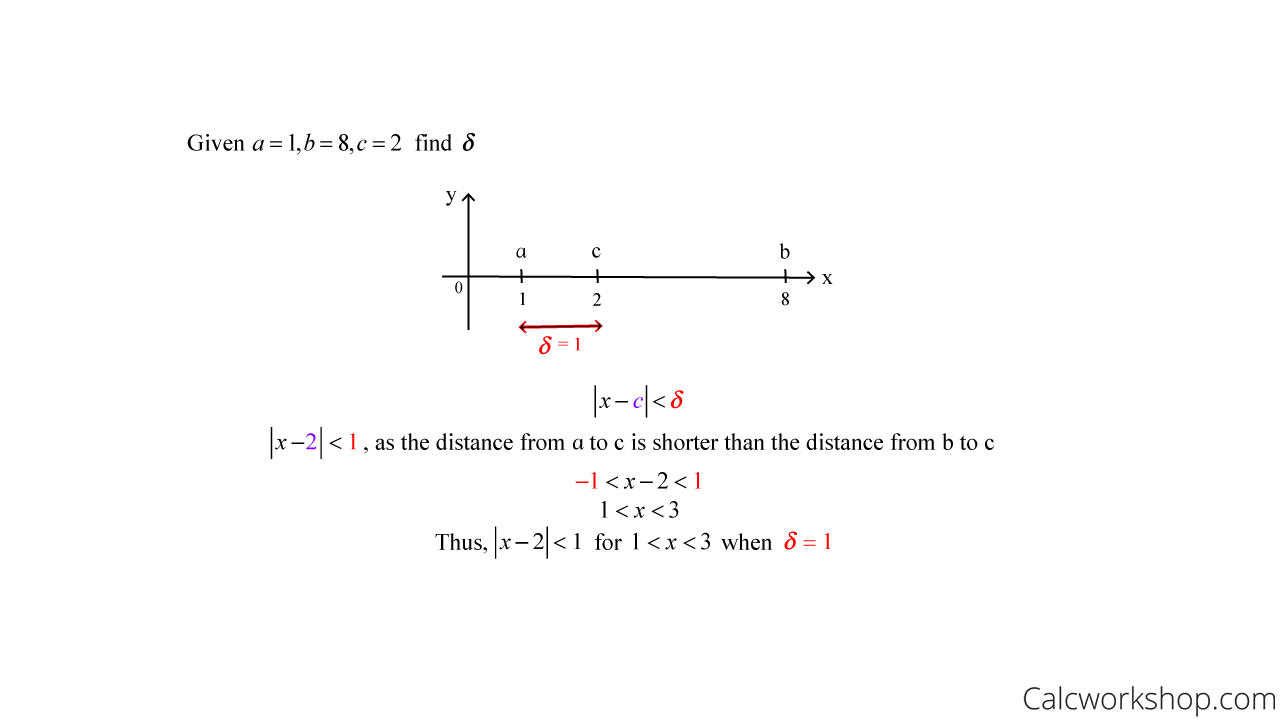
Epsilon Delta Definition Of A Limit Fully Explained

Mathculus Is An Educational Website On Mathematics Where You Can Learn Different Sections Of Calculus Like Fun Maths Algebra Formulas Math Formulas Mathematics

Finding Derivative With Definition Of Derivative Ap Calculus Ab Ap Calculus Calculus

Antiderivative Of Log Integration By Parts Calculus Fractions

Basic Derivative Rules Review Writing Equations Ap Calculus Calculus

Definition Of A Derivative Using Limits Take Limit Of The Slope At A Point Slope F X H F X X H X F X H F X H Mathematiques Amelioration De Soi

Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki Math Calculus College Math

Calculus The Definition Of The Derivative

Calculus Limitsthis Resource Contains 13 Limits By Definition Problems From Calculus 1 Using The Basic Delta Epsilon Method To Find Calculus Ap Calculus Delta