Definition Of Function Cot X
As a formula it can also be written as. Notice that the function is undefined when the tangent function is 0 leading to a vertical asymptote in the graph at 0 pi etc.

To Find The Antiderivative Of Cotx We Will Use Some Identities Of Trigonometry Substitution Method And The Log Identiti Math Methods Studying Math Trigonometry
Cot thetafrac x y cotθ yx Here θ is the angle between the positive x-axis and the line joining the origin to the point xy measured anti-clockwise.
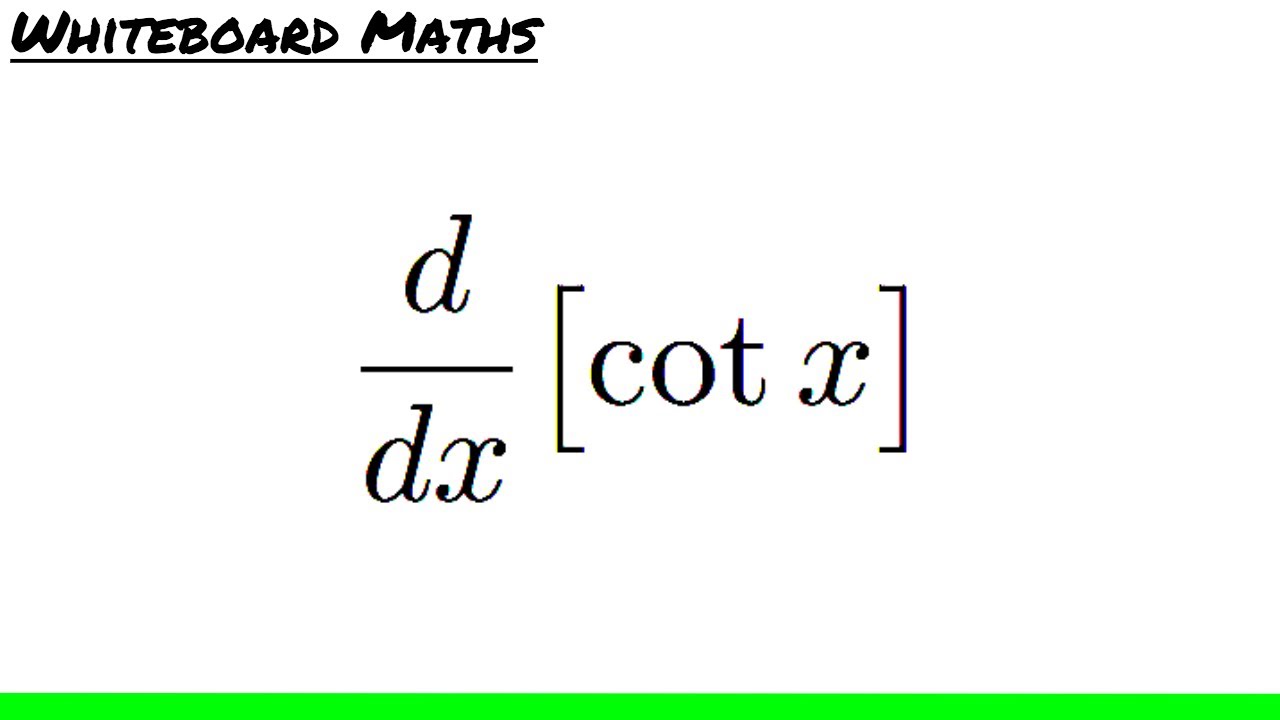
Definition of function cot x. This means that at any value of x the rate of change or slope of cotxis csc2x. Opposite sin hypotenuse q hypotenuse csc opposite q adjacent cos hypotenuse q hypotenuse sec adjacent q opposite tan adjacent q adjacent cot opposite q Unit circle definition For this definition q is any angle. The left window shows the function cscx.
Trigonometric functions are also known as a Circular Functions can be simply defined as the functions of an angle of a triangle. Because the cotangent function is the reciprocal of the tangent function it goes to infinity whenever the tan function is zero and vice versa. This is all assuming that the basic definitions of trigonometric functions are based on ratios of the sides of triangles.
The cotangent is defined by the reciprocal identity cot xdfrac 1 tan x. Sin 1 y qy 1 csc y q cos 1 x qx 1 sec x q. On then right is its derivative -cscxcotx.
X 0 x 0. The basic trigonometric functions are sine cosine tangent cotangent secant and cosecant. This is similar to the rule for sec x but using csc x and cot x plus a minus sign.
We define the following six trigonometric ratios. Coth x cosh x sinh x ex ex ex ex. Cot x 1 cos x tan x sin x Note sec x is not the same as cos -1 x sometimes written as arccos x.
Although the usual notation is cot x the function is sometimes denoted as ctg x. The definition that cot x 1tan x is the shortcut and is not entirely accurate as you pointed out. It is a periodic function repeating with a period π.
Then by the definition x cot y. See also definition of the cosecant csc trigonometric function. It means that the relationship between the angles and sides of a triangle are given by these trig functions.
Cotx is continuous at every point of its domain. Notice that all of the derivatives for co-functions cos cot csc have a minus sign while the derivatives for the other three functions sin tan sec do not. Cosineθ Base Hypotenuse x r and is written as cosθ.
Y we get dxdy - cosec2 y dydx - 1cosec2 y dydx - 11 cot2 y dydx - 11 x2. X π x π. Inverse trigonometric functions are simply defined as the inverse functions of the basic trigonometric functions which are sine cosine tangent cotangent secant and cosecant functions.
In mathematics the inverse trigonometric functions occasionally also called arcus functions antitrigonometric functions or cyclometric functions are the inverse functions of the trigonometric functions with suitably restricted domainsSpecifically they are the inverses of the sine cosine tangent cotangent secant and cosecant functions and are used to obtain an angle from. The last trigonometric function we need to explore is cotangent. In the right-angled ΔAMP Base AM x Perpendicular PM y and Hypotenuse AP r.
So it is a continuous function. Analyzing the Graph of y cot x. Alternatively for a point xy on a unit circle radius is 1 unit in the cartesian co-ordinate system the cotangent function is defined as.
Let y cot-1 x. The derivative of cotx In calculus the derivative of cotxis csc2x. But what about x.
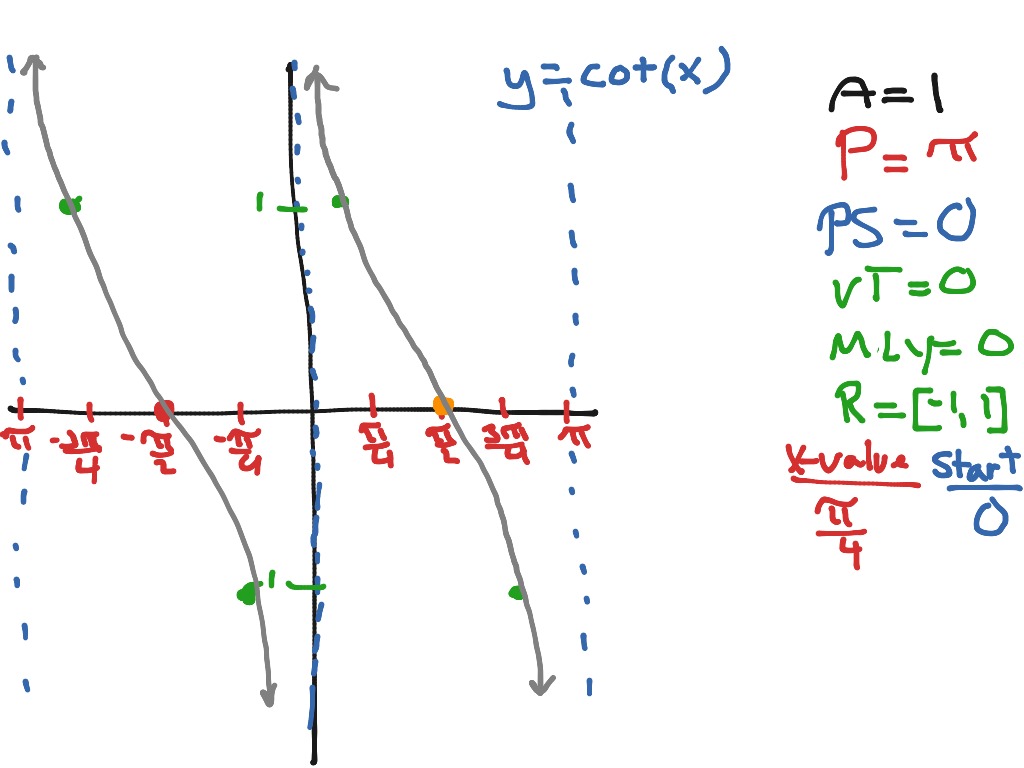
In figure 2 the angle is denoted by t. Hence the derivative of cot-1 x is. The basic period for y cot x y cot x will occur at 0 π 0 π where 0 0 and π π are vertical asymptotes.
The cotangent function cot x is a trigonometric functiona function of angles. Sineθ Perpendicular Hypotenuse y r and is written as sinθ. That is cotx is defined for any real number apart from integer multiples of π.
They are also termed as arcus functions antitrigonometric functions or cyclometric functions. For that matter cot x cos x sin x is also a shortcut. Remember you cannot divide by zero and so these definitions are.
0 π 0 π Find the period π b π b to find where the vertical asymptotes exist. Set the inside of the cotangent function x x equal to π π. Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p.

The Function F X Cot X Is Discontinuous On Set Youtube
Cot Or Ctg Trigonometric Cotangent Function Librow Digital Lcd Dashboards For Cars And Boats

Graphing The Trigonometric Functions Opencurriculum Trigonometric Functions Graphing Function
The Graph Of The Cotangent Function F X Cot X Properties Of The Cotangent Function Zeros Of The Cotangent Function Parity And Periodicity Of The Cotangent Function Behavior Of The Cotangent

Integral Of 1 Tan X Cot X Calculus 1 Calculus Email Subject Lines Mathematics
Calculus I Derivative Of Cotangent Function Cot X Proof Video Dailymotion

Unit Circle Definition Of Trigonometric Functions Trig Functions Circle Definition Trigonometric Functions Math Pictures
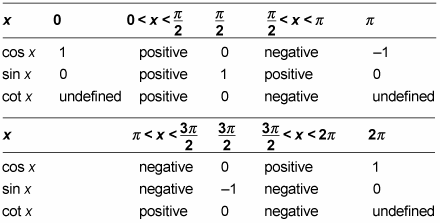
How To Graph A Cotangent Function Dummies
Graph Y Cot X Math Trigonometry Trigonometric Functions Precalculus Showme

Finding A Limit Using L Hopital S Rule X Cot X As X Approaches Zero Math Videos Calculus Theorems

Graphing The Trigonometric Functions Opencurriculum Trigonometric Functions Graphing Function



Post a Comment for "Definition Of Function Cot X"