Definition Of Integer Arithmetic
In Maths integers are the numbers which can be positive negative or zero but cannot be a fraction. The factorial function can also be extended to non-integer arguments.

Properties Of Integers Video Lessons Examples And Solutions
Addition and Subtraction.

Definition of integer arithmetic. These numbers are used to perform various arithmetic operations like addition subtraction multiplication and division. From Latin whole complete. The numbers 4 876 and 5280 are all integers.
3 is a divisor of 12 because 12 3 4 exactly. See tag- in Indo-European roots. For example 8 divided by 3 would yield the whole number 2.
Given the integers a b and n the expression a b mod n pronounced a is congruent to b modulo n means that a b is an integer multiple of n or equivalently a and b both share the same remainder when divided by n. Zero which isnt positive or negative is kept at the center. The most common result of an overflow is that the least significant representable digits of the result are stored.
The number 2 is an example of an integer. The counting numbers 1 2 3 zero 0 and the negative of the counting numbers -1 -2 -3 We can write them all down like this. It is the Latin ablative of modulus which itself means a small measure.
The result is said to. A complete unit or entity. 0 Arithmetic without fractions.
For natural numbers n the arithmetic derivative Dn is defined as follows. Positive numbers are placed on the right side of 0 as they are greater than 0. It is defined recursively as.
A computer performing integer arithmetic ignores any fractions that are derived. For example 8 divided. In other words the division works perfectly with no fractions or remainders involved.
Can the definition of algebraic Integer. A 0 a 1 a S b S a b. See tag-in Indo-European roots.
A computer performing integer arithmetic ignores any fractions that are derived. Negative whole numbers -1 -2 -3. A familiar use of modular arithmetic is in the 12-hour clock in which the day is divided into two.
4 is a divisor of 12 because 12 4 3 exactly. To increase the flexibility of both the FM and ZM packages they have been written so that the type of arithmetic used for the basic operations can be easily changed. Negative whole numbers -1 -2 -3.
D p 1 for any prime p. 2 displaystyle begin aligneda0a textrm 1aS bS ab textrm 2end aligned The structure N is a commutative monoid with identity element 0. The roots of polynomials such as x 3 b x 2 c x d 0 with integer or rational coefficients.
Arithmetic An element of the infinite and numerable set -3-2. Of course arithmetic is important in many cases but Python is probably more. Be accurately paraphrased as.
The number on the right horizontal side is always greater than the left side number. From Latin whole complete. For example 8 divided by 3 would yield the whole number 2.
Integer Arithmetic Hands-on Python Tutorial for Python 3. The value of 0. We start with the integers and integer arithmetic not because arithmetic is exciting but because the symbolism should be mostly familiar.
The factorial operation is encountered in many areas of mathematics notably in combinatorics algebra and mathematical analysisIts most basic use counts the possible distinct sequences the permutations of n distinct objects. And zero 0. A member of the set of positive whole numbers 1 2 3.
A member of the set of positive whole numbers 1 2 3. And zero 0. However some machines are faster using integer arithmetic.
The examples of integers are 1 2 58 -9. A number with no fractional part no decimals. D pq D p q pD q for any p q N displaystyle pqin mathbb N Leibniz rule.
In computer programming an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is outside of the range that can be represented with a given number of digits either higher than the maximum or lower than the minimum representable value. Integer arithmetic Arithmetic without fractions. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae published in 1801.
Any real or complex number A i B where A and B are integers. A number that divides the integer exactly no remainder. A positive or negative whole number or zero.
Negative numbers are placed on the left side of 0 as they are smaller than 0. Is 1 according to the convention for an empty product. In mathematics modular arithmetic is a system of arithmetic for integers where numbers wrap around when reaching a certain value called the modulus.
A computer performing integer arithmetic ignores any fractions that are derived. A complete unit or entity.

Integers And Opposite Numbers Solutions Examples Worksheets Videos Lesson Plans

What Are Integers And Why It Is Important

Arithmetic Mean Examples Solutions Worksheets Videos Games Activities

Division Of Integers Definition Diagram Properties Examples

Integers Multiplication Division Adding Subtracting Rules Positive Negative Numbers Math Youtube

Fundamental Math For The Gmat Properties Of Integers Study Com

Dominie The Educational Suppliers Integers Chart Math Integers Integers Homeschool Math

Integer Formula How To Calculate Integers With Integer Rules
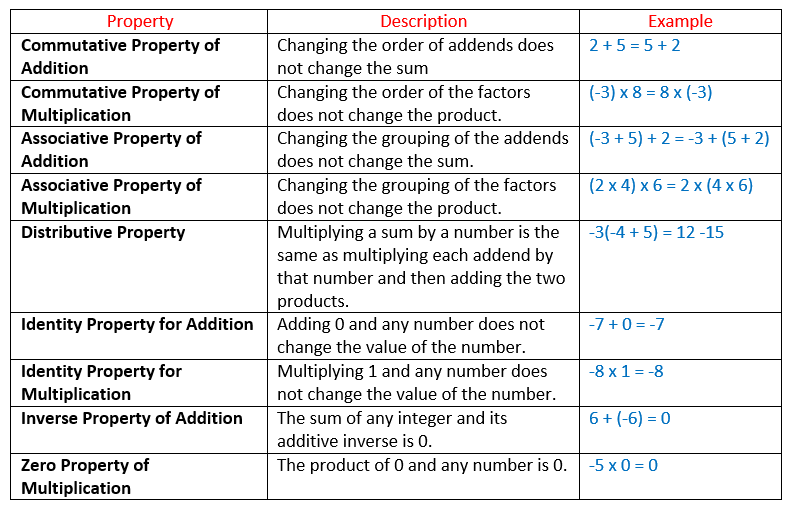
Properties Of Integers Video Lessons Examples And Solutions

Fundamental Math For The Gmat Properties Of Integers Study Com

What Are Integers And Why It Is Important

Positive And Negative Integers Definition Example Representation On Number Line Mathsmd

Definition Of Integer Integers Definitions Mathematics

Integers Definition Properties Examples Of Integers

Arithmetic Definition Facts Examples Cuemath

Numbers Natural Integer Irrational Real Complex

Education Math Teaching Math Math Methods
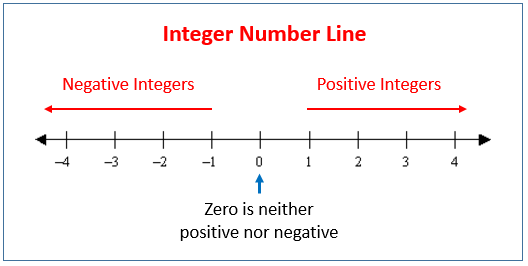
Integer Number Line Video Lessons Examples And Solutions
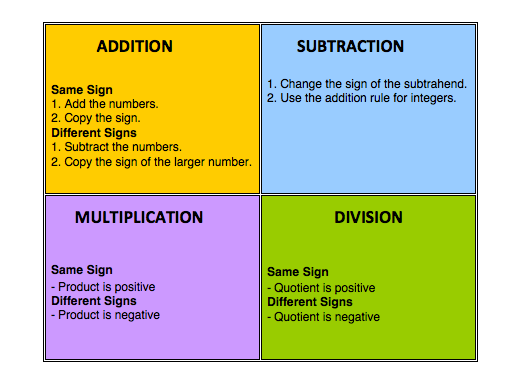
Post a Comment for "Definition Of Integer Arithmetic"